Recursion

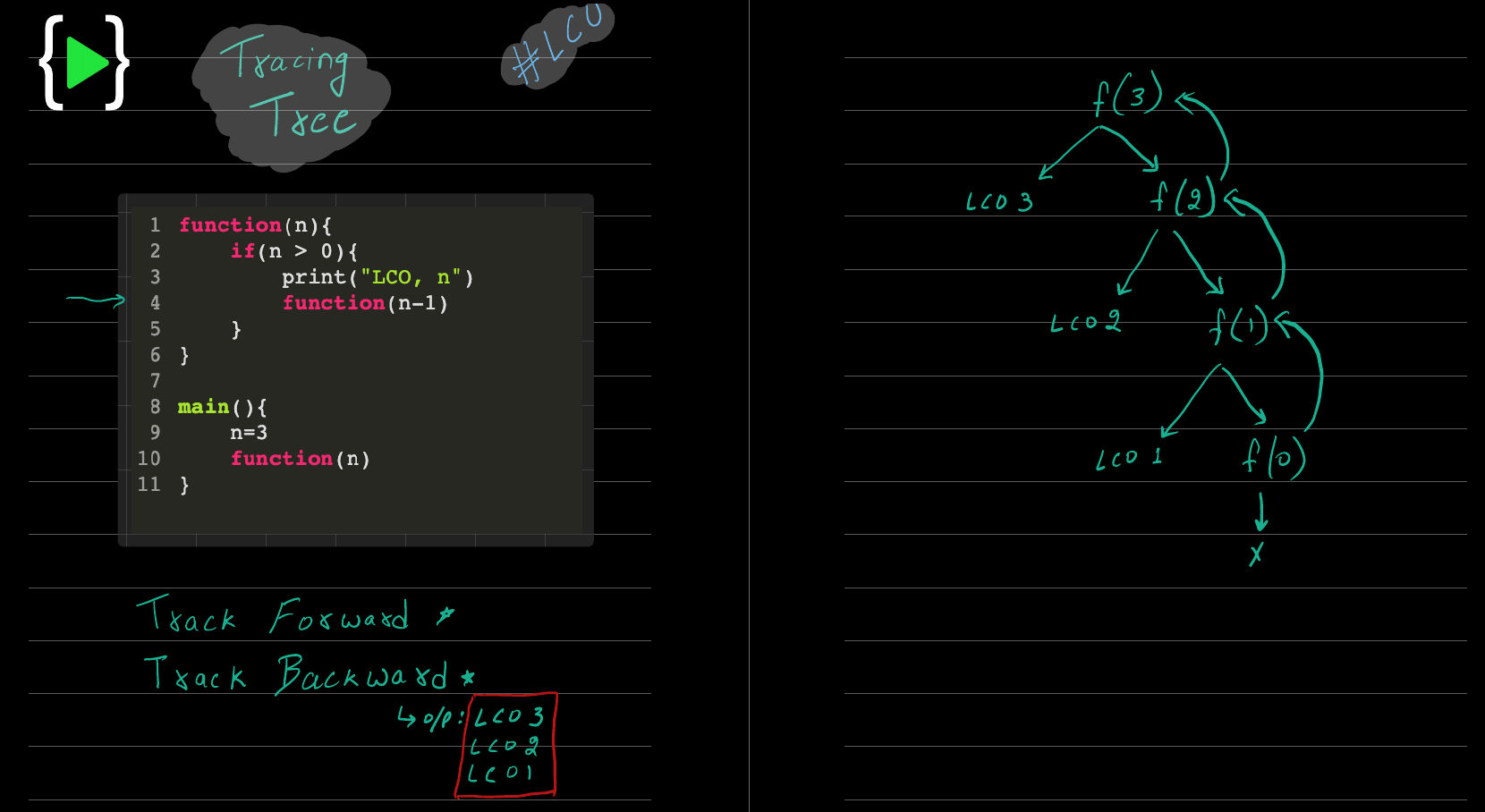
The process in which a function calls itself directly or indirectly with a failure condition is called recursion.

Properties of Recursion:

Performing the same operations multiple times with different inputs.
In every step, we try smaller inputs to make the problem smaller.
Base condition is needed to stop the recursion otherwise infinite loop will occur.

How are recursive functions stored in memory?

Recursion uses more memory, because the recursive function adds to the stack with each recursive call, and keeps the values there until the call is finished. The recursive function uses LIFO structure.

Eg-1

Eg-2

Eg-3

Factorial

def factorial(n):
    if n == 1:
        return 1
    else:
        return n * factorial(n-1)


if __name__ == '__main__':
    print(factorial(5))

Fibonacci Series

def for_fibonacci_series(n):
    nlist = []
    num1, num2 = 0, 1
    for i in range(1, n + 1):
        nlist.append(num1)
        num1, num2 = num2, num1 + num2
    print(nlist)

def recursion_fibonacci_num(n):
    if n <= 1:
        return n
    else:
        return recursion_fibonacci_num(n - 1) + recursion_fibonacci_num(n - 2)

# Not Efficient
def recursion_fibonacci_series(n):
    nlist = []
    for i in range(n):
        nlist.append(recursion_fibonacci_num(i))
    print(nlist)


if __name__ == '__main__':
    for_fibonacci_series(10)
    print(recursion_fibonacci_num(8))
    recursion_fibonacci_series(10)

Power Function

def power_function(base, exp):
    if exp == 1:
        return base
    if exp != 1:
        return base * power_function(base, exp-1)
        
if __name__ == '__main__':
    print(power_function(2, 3))

Tower of Hanoi

Play Tower of Hanoi: https://www.mathsisfun.com/games/towerofhanoi.html

• Move n-1 disk from A to B using C
• Move 1 disk from A to C
• Move n-1 disk from B to C using A